当研究室では，動吸振器を使った多自由度系の制振や複雑な連続体の振動現象の解明に取り組んでおり，以下のようなテーマの研究を行っています．
(1) 一つの動吸振器による複数のモードの同時制振
通常の動吸振器は一つの固有振動数を対象として設計され，複数のモードの制振が必要な場合は制振したいモードの数だけ動吸振器が必要となります．しかし，スペースやコストの問題のために多数の動吸振器を取り付けることが困難な場合も想定されます．
そこで，一つの動吸振器で複数のモードを同時制振することを目指して研究を行っています．
以下の左図のような二自由度系に動吸振器を一つ取り付けた場合に対して，定点理論により動吸振器を設計すると周波数応答関数は以下の右図のようになります．
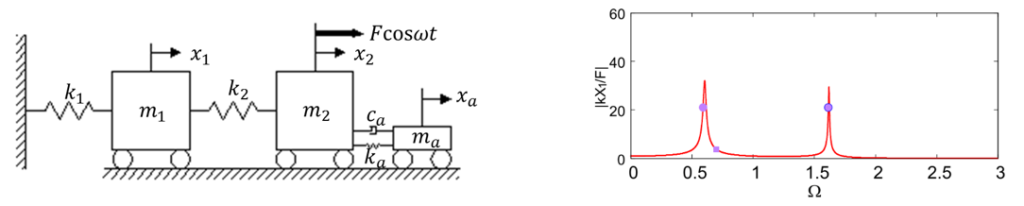動吸振器を一つ取り付けた二自由度系 周波数応答関数（一例）
(2) 三次元直交異方性を有する連続体の振動解析
異方性材料の代表的なものとして炭素繊維強化プラスチック(CFRP)があり，繊維方向を変えて積層した薄板やシェルとして幅広く使われています．一方，未だ実用化はなされていませんが，3Dプリンターなどの発展により積層構造ではなく直方体や厚肉円筒を直接成形することが可能になると考えられます．
そこで，x, y, z軸全ての方向に機械的性質が異なる三次元直交異方性材料の振動解析に取り組んでいます．
そして，以下の左図のような三次元直交異方性を持つ直方体に対して，寸法に対する固有振動数の変化や固有モードの変化などを調べています．
三次元直交異方性を持つ直方体 寸法に対する固有振動数の変化
（島根大学 総合理工学部 S.T）